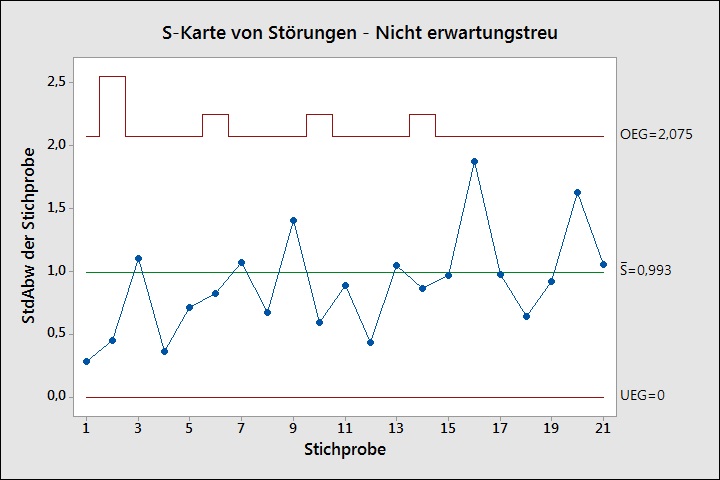
Minitab 22 - Regelkarten und Erwartungstreue (S-Karte)

• Überarbeitet am 8.5.2024
• Software: Minitab 22, 21, 20, 19, 18, 17

In diesem Artikel erklären wir Schritt für Schritt alle Berechnungen, die zu einer Qualitätsregelkarte führen, ausgehend von den reinen Messwerten und Teilgruppeninformationen über:

• Mittelwerte
• zusammengefasster Standardabweichung
• Konstanten für die erwartungstreue Schätzung
• Eingriffsgrenzen

Das APS-Paket Nr. 361 zeigt den Unterschied zwischen einer S-Karte ohne und mit Verwendung einer Konstanten für die erwartungstreue Schätzung. Um die Ergebnisse aus dem Beispiel zu reproduzieren, bitte stellen Sie sicher, dass in den S-Karten-Optionen die Zusammengefasste Standardabweichung ausgewählt ist.

Ziel des Artikels ist, Ihnen ein selbsterklärendes Beispiel zum Nachrechnen des Aufbaus einer Regelkarte bereitzustellen. Wir zeigen den Berechnungshintergrund und insbesondere der Einfluss von erwartungstreuen Schätzern.

Mit diesem Artikel wollen wir ferner Antwort auf folgen Fragen geben:

• Wie wird die zusammengefasste Standardabweichung berechnet?
• Was bedeuten die Konstanten für die erwartungstreue Schätzung und wo fließen diese ein?
• Wie werden Teilgruppeninformationen berücksichtigt?
• Wie werden die Eingriffsgrenzen berechnet?

Beispieldaten:

Der Beispieldatensatz hat 100 Zeilen und 2 Spalten mit der Information:

• Spalte 1: Numerische Messgrößen (Störungen)
• Spalte 2: Teilgruppeninformationen (Schicht)

Es gibt drei Schichten, in denen abwechselnd nacheinander unterschiedlich große Stichprobenmengen gezogen werden. Die Teilgruppen sind daher 1, 2 und 3. Die Teilgruppengröße ist nicht konstant. Das wird durch die zusammengefasste (erwartungstreue) Standardabweichung und die daraus resultierenden Eingriffsgrenzen entsprechend korrigierend aufgezeigt.

↓
C1
C2



 
Störungen
Schicht



1
-0.22435
1



2
0.29532
1



3
0.35517
1



4
-0.2506
1



5
0.0466
1



6
-0.01963
2



7
0.12111
2



8
-0.72188
2



9
-0.77907
3



10
0.08592
3



11
0.85706
3



12
0.76707
3



13
-1.74551
3



14
1.03661
1



15
1.55849
1



16
0.80987
1



17
1.16753
1



18
1.69012
1



19
0.08032
2



20
0.71976
2



21
1.44533
2



22
-0.41543
2



23
0.08678
2



24
0.26149
3



25
-0.18864
3



26
-1.32287
3



27
0.56909
3



28
-0.14831
1



29
-0.3283
1



30
-0.27419
1



31
1.63038
1



32
-1.33516
1



33
0.80181
2



34
-0.88466
2



35
-0.14942
2



36
-0.27939
2



37
0.52527
2



38
1.54787
3



39
1.31244
3



40
-0.75945
3



41
-1.39889
3



42
-1.14574
3



43
1.05937
1



44
0.46393
1



45
-0.24632
1



46
0.93748
1



47
-0.43042
2



48
-1.06083
2



49
-0.00211
2



50
-1.53484
2



51
0.72983
2



52
-0.14778
3



53
0.43946
3



54
-0.70796
3



55
-0.48124
3



56
-0.24787
3



57
0.30332
1



58
0.49884
1



59
-0.90204
1



60
-1.39883
1



61
1.13358
1



62
-0.69206
2



63
0.58544
2



64
1.19559
2



65
1.09305
2



66
0.22087
3



67
-0.51766
3



68
0.60816
3



69
1.37174
3



70
1.96348
3



71
1.63753
1



72
2.20908
1



73
1.12096
1



74
0.69182
1



75
-2.57542
1



76
-1.02231
2



77
0.17477
2



78
-0.78625
2



79
1.44776
2



80
0.14995
2



81
1.00423
3



82
0.52556
3



83
0.27059
3



84
-0.75113
3



85
0.22642
3



86
0.58072
1



87
0.44028
1



88
0.41738
1



89
1.46229
1



90
-1.10618
1



91
-0.24318
2



92
-2.03943
2



93
0.99862
2



94
2.32768
2



95
-0.36141
2



96
-1.14762
3



97
-0.41983
3



98
1.52473
3



99
-0.95736
3



100
-0.17845
3

Das entsprechende APS-Paket ist über unseren ADDITIVE Professional Service erhältlich. Um das Paket zu erhalten, kontaktieren Sie unseren Support per E-Mail an Diese E-Mail-Adresse ist vor Spambots geschützt! Zur Anzeige muss JavaScript eingeschaltet sein. oder per Telefon unter +49 6172 5905 20 jeweils unter Angabe der APS-Paketnummer 361.

Bilder

Ablauf der Berechnungen

Schritt 1a:

Die Teilgruppeninformationen werden fortlaufend berechnet. Daraus ergibt sich die spätere X- Achse der Regelkarte. Im Beispiel führt das Durchnummerieren zu insgesamt 21 verschiedenen Teilgruppen, die wir nachfolgend als Stichproben bezeichnen. Wichtiger Punkt: Basierend auf dieser Zuordnung werden die statistischen Größen berechnet, nicht etwa nur auf der Gruppeninformation Schicht (siehe Arbeitsblatt im Projekt, Spalte StichprobeNr.)

Schritt 1b:

Für jede der fortlaufend durchnummerierten Stichproben wird die Strichprobengröße berechnet (siehe Arbeitsblatt im Projekt, Spalte TGGR1). Im Beispiel:

StichprobenNr
Anzahl



1
5



2
3



3
5



4
5



5
4



6
5



7
5



8
5



9
4



10
5



11
5



12
5



13
4



14
5



15
5



16
5



17
5



18
5



19
5



20
5



21
5

Schritt 1c:

Die Standardabweichungen werden anhand der Zuordnung StichprobenNr. berechnet und eingezeichnet (siehe Arbeitsblatt im Projekt, Spalte DPunkt1).

Schritt 1d:

Die Anzahlen der Freiheitsgerade der Teilgruppen werden ermittelt (siehe Arbeitsblatt im Projekt, Spalte Freiheitsgrade). Die Gesamtanzahl an Freiheitsgraden über alle Teilgruppen im Projekt ist df = 79 (siehe Arbeitsblatt im Projekt, Spalte sum df).

Schritt 2:

Ermittlung der zusammengefassten erwartungstreuen Standardabweichung und Berechnung der Mittellinie der S-Karte
(siehe Arbeitsblatt im Projekt, Spalte STDABWN1). Wenn unter den S-Optionen der Haken Konstante für erwartungstreue Schätzung verwenden gesetzt ist, wird die zusammengefasste Standardabweichung mit einer Konstante für die erwartungstreue Schätzung (unbiasing constant, tabelliert in Minitab) korrigiert.

$s{d}_{pooled\_est}=\frac{s{d}_{pooled}}{c4(df+1)}$

Hier ist $\mathrm{c4}\left(\mathrm{df}+1\right)$ die Konstante für die erwartungstreue Schätzung, und $\mathrm{df}$ bedeutet degrees of freedom, auf Deutsch Freiheitsgrade.

Die noch nicht erwartungstreu korrigierte zusammengefasste Standardabweichung ist:

$sp=0.993428$

Danach werden die Konstanten $\mathrm{c4}\left(\mathrm{df}+1\right)$ für die erwartungstreue Schätzung der zusammengefassten Standardabweichung ermittelt:

$c{4}_{80}=0.996841$

Zusätzlich werden die Konstanten für die erwartungstreue Schätzung für jede Teilgruppe gebildet. Beispielsweise ergibt sich für die Teilgruppengröße 5 der Wert

$c{4}_5=0.939986$

Die erwartungstreue gesamte zusammengefasste Standardabweichung (nicht zu verwechseln mit der Gesamtstandardabweichung) ist also:

$s{p}_e = \frac{sp}{c{4}_{80}}=0.9965762$

Die erwartungstreue zusammengefasste Teilgruppenstandardabweichung sp_ee im Beispiel für die Teilgruppengröße 5 ist also:

$s{p}_{ee}=s{p}_e*c{4}_5=0.9367677$

Man hat es also mit zwei verschiedenen erwartungstreuen Schätzern zu tun, einmal für die gesamte zusammengefasste Standardabweichung, sowie einen zweiten erwartungstreuen Schätzer für die Teilgruppen. Diese Werte finden sich in dem Minitab Arbeitsblatt, sowie grafisch in der S-Karte wieder.

Schritt 3:

Berechnung der Eingriffsgrenzen der S-Karte (siehe Arbeitsblatt im Projekt, Spalten EGRENZ1 und EGRENZ2). Anmerkung: Die Funktion der Konstanten c5 für die erwartungstreue Schätzung ist:

$c5=\sqrt{1-c4(n_i{)}^2}$

Hier ist n_i die Anzahl der Elemente der Teilgruppe.

Berechnung der unteren Eingriffsgrenze (Lower Control Limit LCL) und der oberen Eingriffsgrenze (Upper Control Limit UCL):

• k = vorgegebener Faktor der Anzahl der Standardabweichungen (default:3)
• s = zusammengefasste Standardabweichung (Mittelwerte der (erwartungstreuen) Standardabweichungen, nicht die Standardabweichung der Teilgruppe).
• a = c4(n_i)*s
• b = c5(n_i)*s * k
• LCL = a - b
• UCL = a + b

Fazit:

Der Einfluss der Konstanten für die erwartungstreue Schätzung wirkt sich nicht aus auf

• die dargestellten Standardabweichungen (schwarze Punktlinie, Spalte DPunkt1)

Der Einfluss der Konstanten für die erwartungstreue Schätzung wirkt sich aus auf:

• die zusammengefasste Standardabweichung und damit:
  • die untere Eingriffslinie (rote Linie, Spalte EGRENZ1)
  • die untere Eingriffslinie (rote Linie, Spalte EGRENZ2)
  • die Mittelwertlinie (grüne Linie, Spalte MLINIE1)

Unter Verwendung der Konstanten für die erwartungstreue Schätzung werden die Eingriffslinien wesentlich enger gezogen, als ohne Berücksichtigung dieser Konstanten. Sie sollten sich bewusst sein, dass sich dieser Effekt bei kleinen Stichprobengrößen stark auswirkt.

Dem Artikel liegt ein Minitab Beispielprojekt bei, in welchem wir die Berechnung der statistischen Größen anhand von Beispieldaten darlegen.