Minitab 22 - Versuchsplanung / Regression - Unterschiedliche Ergebnisse bei gleichen Daten
- Erstellt am 11.9.2018
- Überarbeitet am 10.4.2024
- Software1 : Minitab 22, 21, 20, 19, 18
In manchen Fällen, wenn ich
-
einen Versuchsplan sowohl mit einem der drei Werkzeuge
- Statistik: Versuchsplanung (DOE): Screening: Screening-Versuchsplan analysieren
- Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan analysieren
- Statistik: Versuchsplanung (DOE): Wirkungsfläche: Wirkungsflächenversuchsplan analysieren
als auch mit dem Werkzeug
Statistik: Regression: Regression: Regressionsmodell anpassen
analysiere, oder
-
auf einem Datensatz verschiedene Versuchsplantypen mit den Werkzeugen
- Statistik: Versuchsplanung (DOE): Screening: Benutzerspezifischen Screening-Versuchsplan definieren
- Statistik: Versuchsplanung (DOE): Faktoriell: Benutzerspezifischen Faktoriellen Versuchsplan definieren
- Statistik: Versuchsplanung (DOE): Wirkungsfläche: Benutzerspezifischen Wirkungsflächenversuchsplan definieren
definiere und jeweils anschließend in diesem Versuchsplantyp analysiere,
erhalte ich voneinander abweichende Modelle und Signifikanzbewertungen (p-Werte). Warum?
Anmerkung
Als Hilfe für Signifikanzbewertungen werden bei Versuchsplänen je nach Versuchsplantyp verschiedene Effektdiagramme mit ausgegeben, wenn Sie das im Unterdialog Grafiken so festgelegt haben. Siehe hierzu auch:
Pareto-Diagramm der Effekte
Pareto-Diagramm der standardisierten Effekte
Wahrscheinlichkeitsnetz und Halb-Wahrscheinlichkeitsnetz der standardisierten Effekte
Erläuterung
Wenn Sie in einem der oberen beiden Fälle unterschiedliche Ergebnissen bei Regressionskoeffiziente und p-Werte am gleichen Datensatz erhalten, bitte überprüfen Sie
- welche Modellterme Sie in die Analyse mit aufgenommen haben? Beachten Sie dabei insbesondere, dass Sie bei faktoriellen Versuchsplänen Wechselwirkungen höherer Ordnung und bei Wirkungsflächenversuchsplänen quadratische Terme mit in das Modell aufnehmen können.
-
mit welcher Kodierung intern gerechnet wird. Bei einem Versuchsplan können Sie sich die Faktoren in kodierten Einheiten anzeigen lassen. Wählen Sie dazu Statistik: Versuchsplanung (DOE): Versuchsplan anzeigen und setzen Sie im Dialogfeld Versuchsplan anzeigen die Option Kodiert als Einheiten für Faktoren.
Weitere Informationen finden Sie im Artikel Versuchsplanung (DOE): Kodierte und nicht kodierte Einheiten.
Wir zeigen hier einige Beispiele mit anfangs unterschiedlichen Ergebnissen.
Beispiel: 2-stufigen faktoriellen Versuchsplan analysieren versus Regressionsmodell anpassen
Den Versuchsplan zum ersten Beispiel haben wir über Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan erstellen erstellt.
Versuchspläne
Faktoren
Vollfaktorieller Versuchsplan
Übersicht des Versuchsplans
|
Faktoren: |
3 |
Basisversuchsplan: |
3; 8 |
|
Durchläufe: |
16 |
Replikationen: |
2 |
|
Blöcke: |
1 |
Zentralpunkte (gesamt): |
0 |
Alle Terme ohne Aliasstruktur.
Die Analyse haben wir zunächst mit dem Werkzeug Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan analysieren durchgeführt.
Terme
Die Koeffizienten und die p-Werte haben wir in der Sessionfensterausgabe hervorgehoben, damit Sie diese später mit den anderen Koeffizienten vergleichen können. Auch die Varianzinflationsfaktoren (VIF) haben wir hervorgehoben.
Faktorielle Regression: Antwort vs. A; B; C
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Modell |
7 |
3294,89 |
470,70 |
941,85 |
0,000 |
|
Linear |
3 |
2761,00 |
920,33 |
1841,55 |
0,000 |
|
A |
1 |
1629,19 |
1629,19 |
3259,94 |
0,000 |
|
B |
1 |
492,23 |
492,23 |
984,93 |
0,000 |
|
C |
1 |
639,57 |
639,57 |
1279,76 |
0,000 |
|
2-Faktor-Wechselwirkungen |
3 |
533,86 |
177,95 |
356,08 |
0,000 |
|
A*B |
1 |
171,37 |
171,37 |
342,91 |
0,000 |
|
A*C |
1 |
208,49 |
208,49 |
417,18 |
0,000 |
|
B*C |
1 |
154,00 |
154,00 |
308,14 |
0,000 |
|
3-Faktor-Wechselwirkungen |
1 |
0,03 |
0,03 |
0,06 |
0,811 |
|
A*B*C |
1 |
0,03 |
0,03 |
0,06 |
0,811 |
|
Fehler |
8 |
4,00 |
0,50 |
|
|
|
Gesamt |
15 |
3298,88 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
0,706938 |
99,88% |
99,77% |
99,52% |
Kodierte Koeffizienten
|
Term |
Effekt |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
|
-5,661 |
0,177 |
-32,03 |
0,000 |
|
|
A |
20,182 |
10,091 |
0,177 |
57,10 |
0,000 |
1,00 |
|
B |
-11,093 |
-5,547 |
0,177 |
-31,38 |
0,000 |
1,00 |
|
C |
12,645 |
6,322 |
0,177 |
35,77 |
0,000 |
1,00 |
|
A*B |
-6,545 |
-3,273 |
0,177 |
-18,52 |
0,000 |
1,00 |
|
A*C |
7,220 |
3,610 |
0,177 |
20,42 |
0,000 |
1,00 |
|
B*C |
-6,205 |
-3,102 |
0,177 |
-17,55 |
0,000 |
1,00 |
|
A*B*C |
0,087 |
0,044 |
0,177 |
0,25 |
0,811 |
1,00 |
Regressionsgleichung in nicht kodierten Einheiten
|
Antwort |
= |
-361,4 - 249,7 A + 7,392 B + 4,452 C - 0,202 A*B + 3,536 A*C - 0,0981 B*C |
Aliasstruktur
|
Faktor |
Name |
|
A |
A |
|
B |
B |
|
C |
C |
|
Aliase |
|
I |
|
A |
|
B |
|
C |
|
AB |
|
AC |
|
BC |
|
ABC |
Zum Vergleich würde sich hier das Anpassen eines Modells mit dem Werkzeug Statistik: Regression: Regression: Regressionsmodell anpassen anbieten.
Damit die Menge der in das Modell aufgenommenen Terme mit der vorherigen Analyse übereinstimmt, müssen Sie auf den Button Modell klicken und die Wechselwirkungen bis zur Ordnung 3 der vorher von Ihnen markierten Prädiktoren A, B und C zu den Termen im Modell hinzufügen.
Die Koeffizienten und p-Werte stimmen nicht mit denen des vorher angepassten Modells überein, und die Varianzinflationsfaktoren sind sehr hoch, was auf große Multikolinearitäten hindeutet.
Regressionsanalyse: Antwort vs. A; B; C
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Regression |
7 |
3294,89 |
470,698 |
941,85 |
0,000 |
|
A |
1 |
46,50 |
46,499 |
93,04 |
0,000 |
|
B |
1 |
32,83 |
32,827 |
65,68 |
0,000 |
|
C |
1 |
16,64 |
16,638 |
33,29 |
0,000 |
|
A*B |
1 |
0,12 |
0,122 |
0,24 |
0,634 |
|
A*C |
1 |
52,49 |
52,492 |
105,03 |
0,000 |
|
B*C |
1 |
32,56 |
32,560 |
65,15 |
0,000 |
|
A*B*C |
1 |
0,03 |
0,031 |
0,06 |
0,811 |
|
Fehler |
8 |
4,00 |
0,500 |
|
|
|
Gesamt |
15 |
3298,88 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
0,706938 |
99,88% |
99,77% |
99,52% |
Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
-361,4 |
57,9 |
-6,24 |
0,000 |
|
|
A |
-249,7 |
25,9 |
-9,65 |
0,000 |
21446,71 |
|
B |
7,392 |
0,912 |
8,10 |
0,000 |
28130,00 |
|
C |
4,452 |
0,772 |
5,77 |
0,000 |
19,06 |
|
A*B |
-0,202 |
0,408 |
-0,49 |
0,634 |
43950,71 |
|
A*C |
3,536 |
0,345 |
10,25 |
0,000 |
21461,96 |
|
B*C |
-0,0981 |
0,0122 |
-8,07 |
0,000 |
28144,06 |
|
A*B*C |
0,00135 |
0,00544 |
0,25 |
0,811 |
43961,96 |
Regressionsgleichung
|
Antwort |
= |
-361,4 - 249,7 A + 7,392 B + 4,452 C - 0,202 A*B + 3,536 A*C - 0,0981 B*C |
Informationen zur Rolle der Varianzinflationsfaktoren finden Sie im Artikel Berechnung von Varianzinflationsfaktoren (VIF).
Der Grund für die unterschiedlichen Ergebnisse ist, dass das Werkzeug Faktoriellen Versuchsplan analysieren mit den auf -1 und 1 kodierten Tief- und Hochwerten der Faktoren rechnet. Auch das Werkzeug Regressionsmodell anpassen bietet die Möglichkeit einer Kodierung. Wenn Sie im Hauptdialog auf den Button Kodierung klicken, für Stetige Prädiktoren standardisieren anschließend die Option Kodierung von -1 bzw. +1 für tiefe bzw. hohe Stufe festlegen auswählen und die gleichen Tief- und Hoch-Werte angeben, wie beim Erstellen des Versuchsplans,
dann stimmen die Koeffizienten und p-Werte (sowie die Varianzinflationsfaktoren) wieder mit denen in der ersten Analyse überein:
Regressionsanalyse: Antwort vs. A; B; C
Methode
Standardisierung der stetigen Prädiktoren
Stufen kodiert mit -1 und +1
|
Prädiktor |
Tief |
Hoch |
|
A |
1 |
3 |
|
B |
22 |
87 |
|
C |
74 |
76 |
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Regression |
7 |
3294,89 |
470,70 |
941,85 |
0,000 |
|
A |
1 |
1629,19 |
1629,19 |
3259,94 |
0,000 |
|
B |
1 |
492,23 |
492,23 |
984,93 |
0,000 |
|
C |
1 |
639,57 |
639,57 |
1279,76 |
0,000 |
|
A*B |
1 |
171,37 |
171,37 |
342,91 |
0,000 |
|
A*C |
1 |
208,49 |
208,49 |
417,18 |
0,000 |
|
B*C |
1 |
154,00 |
154,00 |
308,14 |
0,000 |
|
A*B*C |
1 |
0,03 |
0,03 |
0,06 |
0,811 |
|
Fehler |
8 |
4,00 |
0,50 |
|
|
|
Gesamt |
15 |
3298,88 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
0,706938 |
99,88% |
99,77% |
99,52% |
Kodierte Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
-5,661 |
0,177 |
-32,03 |
0,000 |
|
|
A |
10,091 |
0,177 |
57,10 |
0,000 |
1,00 |
|
B |
-5,547 |
0,177 |
-31,38 |
0,000 |
1,00 |
|
C |
6,322 |
0,177 |
35,77 |
0,000 |
1,00 |
|
A*B |
-3,273 |
0,177 |
-18,52 |
0,000 |
1,00 |
|
A*C |
3,610 |
0,177 |
20,42 |
0,000 |
1,00 |
|
B*C |
-3,102 |
0,177 |
-17,55 |
0,000 |
1,00 |
|
A*B*C |
0,044 |
0,177 |
0,25 |
0,811 |
1,00 |
Regressionsgleichung in nicht kodierten Einheiten
|
Antwort |
= |
-361,4 - 249,7 A + 7,392 B + 4,452 C - 0,202 A*B + 3,536 A*C - 0,0981 B*C |
Beispiel: Wirkungsflächenversuchsplan analysieren versus 2-stufigen faktoriellen Versuchsplan analysieren
Den Versuchsplan zum zweiten Beispiel haben wir über Statistik: Versuchsplanung (DOE): Wirkungsflächenversuchsplan erstellen erstellt.
Versuchspläne
Faktoren
Zentral zusammengesetzter Versuchsplan
Übersicht des Versuchsplans
|
Faktoren: |
3 |
Replikationen: |
2 |
|
Basisdurchläufe: |
20 |
Durchläufe gesamt: |
40 |
|
Basisblöcke: |
1 |
Blöcke gesamt: |
1 |
α = 1,68179
Zweistufig faktoriell: vollfaktoriell
Punkttypen
|
Würfelpunkte: |
16 |
|
Zentralpunkte im Würfel: |
12 |
|
Sternpunkte: |
12 |
|
Zentralpunkte axial: |
0 |
Die Analyse haben wir zunächst mit dem Werkzeug Statistik: Versuchsplanung (DOE): Wirkungsfläche: Wirkungsflächenversuchsplan analysieren durchgeführt
Terme
Regression für Wirkungsfläche: Antwort vs. A; B; C
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Modell |
6 |
1892,29 |
315,382 |
300,01 |
0,000 |
|
Linear |
3 |
1089,84 |
363,281 |
345,57 |
0,000 |
|
A |
1 |
104,71 |
104,711 |
99,61 |
0,000 |
|
B |
1 |
143,77 |
143,773 |
136,76 |
0,000 |
|
C |
1 |
841,36 |
841,358 |
800,34 |
0,000 |
|
2-Faktor-Wechselwirkung |
3 |
802,45 |
267,483 |
254,44 |
0,000 |
|
A*B |
1 |
632,89 |
632,886 |
602,03 |
0,000 |
|
A*C |
1 |
131,23 |
131,226 |
124,83 |
0,000 |
|
B*C |
1 |
38,34 |
38,337 |
36,47 |
0,000 |
|
Fehler |
33 |
34,69 |
1,051 |
|
|
|
Fehlende Anpassung |
8 |
7,59 |
0,949 |
0,88 |
0,550 |
|
Reiner Fehler |
25 |
27,10 |
1,084 |
|
|
|
Gesamt |
39 |
1926,98 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
1,02530 |
98,20% |
97,87% |
97,52% |
Kodierte Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
4,457 |
0,162 |
27,49 |
0,000 |
|
|
A |
1,958 |
0,196 |
9,98 |
0,000 |
1,00 |
|
B |
-2,294 |
0,196 |
-11,69 |
0,000 |
1,00 |
|
C |
-5,550 |
0,196 |
-28,29 |
0,000 |
1,00 |
|
A*B |
-6,289 |
0,256 |
-24,54 |
0,000 |
1,00 |
|
A*C |
2,864 |
0,256 |
11,17 |
0,000 |
1,00 |
|
B*C |
-1,548 |
0,256 |
-6,04 |
0,000 |
1,00 |
Regressionsgleichung in nicht kodierten Einheiten
|
Antwort |
= |
-155,2 + 0,523 A + 12,74 B + 1,100 C - 0,08827 A*B + 0,01827 A*C - 0,1126 B*C |
Anpassungen und Bewertung für ungewöhnliche Beobachtungen
|
Beob |
Antwort |
Anpassung |
Resid |
Std. |
|
|
19 |
-1,831 |
0,599 |
-2,429 |
-2,54 |
R |
R Großes Residuum
Sie könnten zum Vergleich den Versuchsplan zu einem faktoriellen Versuchsplan umdefinieren (Statistik: Versuchsplanung (DOE): Faktoriell: Benutzerspezifischen faktoriellen Versuchsplan definieren).
Sie müssen den Button Tief/Hoch klicken, um den Versuchsplan definieren zu können. Das Programm schlägt Ihnen hier Werte vor. Wir werden sehen, welches Ergebnis wir bekommen, wenn Sie diese Werte nicht verändern.
Damit die Spalten mit Standardreihenfolge, Durchlaufreihenfolge und Blöcken nicht erneut erstellt werden, können Sie im Hauptdialog den Button Versuchspläne anklicken und die bereits vorhandenen Spalten dort angeben.
Jetzt können Sie den Versuchsplan analysieren.
Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan analysieren
Terme
Auch hier stimmen die Koeffizienten nicht mit denen der ersten Analyse überein.
Faktorielle Regression: Antwort vs. A; B; C
* HINWEIS * Die Daten im Arbeitsblatt entsprechen möglicherweise nicht den für den
Versuchsplan angegebenen Einheiten und/oder Stufen.
* HINWEIS * Dieser Versuchsplan weist einige misslungene Durchläufe auf.
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Modell |
6 |
1892,29 |
315,382 |
300,01 |
0,000 |
|
Linear |
3 |
1089,84 |
363,281 |
345,57 |
0,000 |
|
A |
1 |
104,71 |
104,711 |
99,61 |
0,000 |
|
B |
1 |
143,77 |
143,773 |
136,76 |
0,000 |
|
C |
1 |
841,36 |
841,358 |
800,34 |
0,000 |
|
2-Faktor-Wechselwirkungen |
3 |
802,45 |
267,483 |
254,44 |
0,000 |
|
A*B |
1 |
632,89 |
632,886 |
602,03 |
0,000 |
|
A*C |
1 |
131,23 |
131,226 |
124,83 |
0,000 |
|
B*C |
1 |
38,34 |
38,337 |
36,47 |
0,000 |
|
Fehler |
33 |
34,69 |
1,051 |
|
|
|
Fehlende Anpassung |
8 |
7,59 |
0,949 |
0,88 |
0,550 |
|
Reiner Fehler |
25 |
27,10 |
1,084 |
|
|
|
Gesamt |
39 |
1926,98 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
1,02530 |
98,20% |
97,87% |
97,52% |
Kodierte Koeffizienten
|
Term |
Effekt |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
|
4,457 |
0,162 |
27,49 |
0,000 |
|
|
A |
6,586 |
3,293 |
0,330 |
9,98 |
0,000 |
1,00 |
|
B |
-7,717 |
-3,859 |
0,330 |
-11,69 |
0,000 |
1,00 |
|
C |
-18,668 |
-9,334 |
0,330 |
-28,29 |
0,000 |
1,00 |
|
A*B |
-35,578 |
-17,789 |
0,725 |
-24,54 |
0,000 |
1,00 |
|
A*C |
16,200 |
8,100 |
0,725 |
11,17 |
0,000 |
1,00 |
|
B*C |
-8,756 |
-4,378 |
0,725 |
-6,04 |
0,000 |
1,00 |
Regressionsgleichung in nicht kodierten Einheiten
|
Antwort |
= |
-155,2 + 0,523 A + 12,74 B + 1,100 C - 0,08827 A*B + 0,01827 A*C - 0,1126 B*C |
Aliasstruktur
|
Faktor |
Name |
|
A |
A |
|
B |
B |
|
C |
C |
|
Aliase |
|
I |
|
A |
|
B |
|
C |
|
AB |
|
AC |
|
BC |
Anpassungen und Bewertung für ungewöhnliche Beobachtungen
|
Beob |
Antwort |
Anpassung |
Resid |
Std. |
|
|
19 |
-1,831 |
0,599 |
-2,429 |
-2,54 |
R |
R Großes Residuum
Der Grund ist: Beim Definieren des faktoriellen Versuchsplans müssen Sie diejenigen Tief- und Hoch-Werte angeben, die den Würfelpunkten (nicht Sternpunkten) entsprechen, mit denen wir den Versuchsplan erstellt haben.
Damit die Spalte für die Zentralpunkte nicht erneut erstellt wird, können Sie diese im Unterdialog Versuchspläne angeben.
Wenn Sie jetzt den faktoriellen Versuchsplan erneut mit den gleichen Modelltermen analysieren, stimmen die Koeffizienten mit denen in der ersten Analyse überein.
Faktorielle Regression: Antwort vs. A; B; C
* HINWEIS * Dieser Versuchsplan weist einige misslungene Durchläufe auf.
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Modell |
6 |
1892,29 |
315,382 |
300,01 |
0,000 |
|
Linear |
3 |
1089,84 |
363,281 |
345,57 |
0,000 |
|
A |
1 |
104,71 |
104,711 |
99,61 |
0,000 |
|
B |
1 |
143,77 |
143,773 |
136,76 |
0,000 |
|
C |
1 |
841,36 |
841,358 |
800,34 |
0,000 |
|
2-Faktor-Wechselwirkungen |
3 |
802,45 |
267,483 |
254,44 |
0,000 |
|
A*B |
1 |
632,89 |
632,886 |
602,03 |
0,000 |
|
A*C |
1 |
131,23 |
131,226 |
124,83 |
0,000 |
|
B*C |
1 |
38,34 |
38,337 |
36,47 |
0,000 |
|
Fehler |
33 |
34,69 |
1,051 |
|
|
|
Fehlende Anpassung |
8 |
7,59 |
0,949 |
0,88 |
0,550 |
|
Reiner Fehler |
25 |
27,10 |
1,084 |
|
|
|
Gesamt |
39 |
1926,98 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
1,02530 |
98,20% |
97,87% |
97,52% |
Kodierte Koeffizienten
|
Term |
Effekt |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
|
4,457 |
0,162 |
27,49 |
0,000 |
|
|
A |
3,916 |
1,958 |
0,196 |
9,98 |
0,000 |
1,00 |
|
B |
-4,589 |
-2,294 |
0,196 |
-11,69 |
0,000 |
1,00 |
|
C |
-11,100 |
-5,550 |
0,196 |
-28,29 |
0,000 |
1,00 |
|
A*B |
-12,579 |
-6,289 |
0,256 |
-24,54 |
0,000 |
1,00 |
|
A*C |
5,728 |
2,864 |
0,256 |
11,17 |
0,000 |
1,00 |
|
B*C |
-3,096 |
-1,548 |
0,256 |
-6,04 |
0,000 |
1,00 |
Regressionsgleichung in nicht kodierten Einheiten
|
Antwort |
= |
-155,2 + 0,523 A + 12,74 B + 1,100 C - 0,08827 A*B + 0,01827 A*C - 0,1126 B*C |
Aliasstruktur
|
Faktor |
Name |
|
A |
A |
|
B |
B |
|
C |
C |
|
Aliase |
|
I |
|
A |
|
B |
|
C |
|
AB |
|
AC |
|
BC |
Anpassungen und Bewertung für ungewöhnliche Beobachtungen
|
Beob |
Antwort |
Anpassung |
Resid |
Std. |
|
|
19 |
-1,831 |
0,599 |
-2,429 |
-2,54 |
R |
R Großes Residuum
Beispiel: Allgemeinen vollfaktoriellen Versuchsplan analysieren versus Regressionsmodell anpassen
Den Versuchsplan zum dritten Beispiel haben wir über Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan erstellen erstellt.
Versuchspläne
Faktoren
Mehrstufiger faktorieller Versuchsplan
Übersicht des Versuchsplans
|
Faktoren: |
2 |
Replikationen: |
2 |
|
Basisdurchläufe: |
9 |
Durchläufe gesamt: |
18 |
|
Basisblöcke: |
1 |
Blöcke gesamt: |
1 |
Anzahl der Stufen: 3; 3
Die Analyse haben wir zunächst mit dem Werkzeug Statistik: Versuchsplanung (DOE): Faktoriell: Faktoriellen Versuchsplan analysieren durchgeführt.
Terme
Allgemeine faktorielle Regression: Antwort vs. A; B
Faktorinformationen
|
Faktor |
Stufen |
Werte |
|
A |
3 |
7; 68; 89 |
|
B |
3 |
90; 95; 98 |
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Modell |
8 |
964,554 |
120,569 |
168,10 |
0,000 |
|
Linear |
4 |
380,726 |
95,182 |
132,70 |
0,000 |
|
A |
2 |
63,432 |
31,716 |
44,22 |
0,000 |
|
B |
2 |
317,295 |
158,647 |
221,19 |
0,000 |
|
2-Faktor-Wechselwirkungen |
4 |
583,827 |
145,957 |
203,50 |
0,000 |
|
A*B |
4 |
583,827 |
145,957 |
203,50 |
0,000 |
|
Fehler |
9 |
6,455 |
0,717 |
|
|
|
Gesamt |
17 |
971,009 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
0,846903 |
99,34% |
98,74% |
97,34% |
Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
5,628 |
0,200 |
28,20 |
0,000 |
|
|
A |
|
|
|
|
|
|
7 |
1,369 |
0,282 |
4,85 |
0,001 |
1,33 |
|
68 |
-2,654 |
0,282 |
-9,40 |
0,000 |
1,33 |
|
B |
|
|
|
|
|
|
90 |
-5,924 |
0,282 |
-20,98 |
0,000 |
1,33 |
|
95 |
2,609 |
0,282 |
9,24 |
0,000 |
1,33 |
|
A*B |
|
|
|
|
|
|
7 90 |
4,687 |
0,399 |
11,74 |
0,000 |
1,78 |
|
7 95 |
-9,676 |
0,399 |
-24,24 |
0,000 |
1,78 |
|
68 90 |
-7,252 |
0,399 |
-18,16 |
0,000 |
1,78 |
|
68 95 |
8,784 |
0,399 |
22,00 |
0,000 |
1,78 |
Regressionsgleichung
|
Antwort |
= |
5,628 + 1,369 A_7 - 2,654 A_68 + 1,285 A_89 - 5,924 B_90 + 2,609 B_95 + 3,315 B_98 |
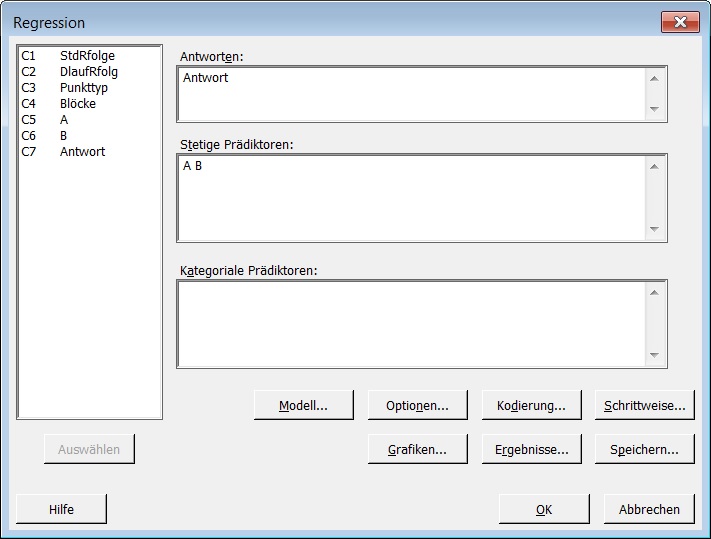
Wenn Sie den Versuchsplan mit dem Werkzeug Statistik: Regression: Regression: Regressionsmodell anpassen, A und B als stetige Prädiktoren angeben,
und die Modellterme A, B und A*B auswählen
erhalten Sie von der ersten Anpassung verschiedene Koeffizienten:
Regressionsanalyse: Antwort vs. A; B
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Regression |
3 |
292,790 |
97,597 |
2,01 |
0,158 |
|
A |
1 |
0,040 |
0,040 |
0,00 |
0,977 |
|
B |
1 |
81,005 |
81,005 |
1,67 |
0,217 |
|
A*B |
1 |
0,014 |
0,014 |
0,00 |
0,987 |
|
Fehler |
14 |
678,218 |
48,444 |
|
|
|
Fehlende Anpassung |
5 |
671,763 |
134,353 |
187,32 |
0,000 |
|
Reiner Fehler |
9 |
6,455 |
0,717 |
|
|
|
Gesamt |
17 |
971,009 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
6,96018 |
30,15% |
15,19% |
0,00% |
Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
-106,5 |
87,4 |
-1,22 |
0,243 |
|
|
A |
-0,04 |
1,35 |
-0,03 |
0,977 |
818,23 |
|
B |
1,198 |
0,926 |
1,29 |
0,217 |
3,47 |
|
A*B |
0,0002 |
0,0143 |
0,02 |
0,987 |
820,71 |
Regressionsgleichung
|
Antwort |
= |
-106,5 - 0,04 A + 1,198 B + 0,0002 A*B |
Um die Ergebnisse der ersten Analyse zu reproduzieren, müssen Sie A und B als Kategoriale Prädiktoren auswählen.
Nachdem Sie sichergestellt haben, dass das Modell die Terme A, B und A*B enthält, und im Unterdialog Regression: Kodierung (-1; 0; +1) als Kodierung für kategoriale Prädiktoren ausgewählt haben,
erhalten Sie die gleichen Koeffizienten wie in der ersten Analyse:
Regressionsanalyse: Antwort vs. A; B
Methode
|
Kodierung der kategorialen Prädiktoren |
(-1; 0; +1) |
Varianzanalyse
|
Quelle |
DF |
Kor SS |
Kor MS |
F-Wert |
p-Wert |
|
Regression |
8 |
964,554 |
120,569 |
168,10 |
0,000 |
|
A |
2 |
63,432 |
31,716 |
44,22 |
0,000 |
|
B |
2 |
317,295 |
158,647 |
221,19 |
0,000 |
|
A*B |
4 |
583,827 |
145,957 |
203,50 |
0,000 |
|
Fehler |
9 |
6,455 |
0,717 |
|
|
|
Gesamt |
17 |
971,009 |
|
|
|
Zusammenfassung des Modells
|
S |
R-Qd |
R-Qd(kor) |
R-Qd(prog) |
|
0,846903 |
99,34% |
98,74% |
97,34% |
Koeffizienten
|
Term |
Koef |
SE Koef |
t-Wert |
p-Wert |
VIF |
|
Konstante |
5,628 |
0,200 |
28,20 |
0,000 |
|
|
A |
|
|
|
|
|
|
7 |
1,369 |
0,282 |
4,85 |
0,001 |
1,33 |
|
68 |
-2,654 |
0,282 |
-9,40 |
0,000 |
1,33 |
|
B |
|
|
|
|
|
|
90 |
-5,924 |
0,282 |
-20,98 |
0,000 |
1,33 |
|
95 |
2,609 |
0,282 |
9,24 |
0,000 |
1,33 |
|
A*B |
|
|
|
|
|
|
7 90 |
4,687 |
0,399 |
11,74 |
0,000 |
1,78 |
|
7 95 |
-9,676 |
0,399 |
-24,24 |
0,000 |
1,78 |
|
68 90 |
-7,252 |
0,399 |
-18,16 |
0,000 |
1,78 |
|
68 95 |
8,784 |
0,399 |
22,00 |
0,000 |
1,78 |
Regressionsgleichung
|
Antwort |
= |
5,628 + 1,369 A_7 - 2,654 A_68 + 1,285 A_89 - 5,924 B_90 + 2,609 B_95 + 3,315 B_98 |
Der Artikel Koeffizienten in einem allgemeinen vollfaktoriellen Versuchsplan erläutert die Berechnung der Koeffizienten und die Verwendung dieser zum Berechnen der Anpassungen in einem allgemeinen vollfaktoriellen Versuchsplan.
Binäre Antwort in einem faktoriellen Versuchsplan analysieren
In Minitab 19 wurde dem Menü Statistik: Versuchsplanung (DOE): Faktoriell der Menüpunkt Binäre Antwort analysieren ergänzt.
Wenn Sie die Ergebnisse der Analyse der binären Antwort am faktoriellen Versuchsplan mit dem Werkzeug
Statistik: Regression: Binäre logistische Regression: Binäres logistisches Modell anpassen
nachvollziehen wollen, müssen Sie dabei darauf achten, dass
- ähnlich wie im Fall der Regression mit einer stetigen Antwort die Kodierungen entsprechend gesetzt und
- der standardmäßig in der gewöhnlichen binären logistischen Regression festgelegte Wald-Test in den Likelihood-Quotienten-Test als Test für die ANOVA-Tabelle geändert wird, damit Sie die Chi-Quadrat-Werte reproduzieren können.
|
|
Download
1Anmerkung zu Minitab 18: Wenn Sie wissen wollen, mit welchen Hoch- und Tief-Werten ein Versuchsplan erstellt oder auf einem existierenden Datensatz benutzerspezifisch definiert wurde, können Sie sich diese zusammen mit weiteren Informationen durch einen Klick auf das Symbol Versuchsplan anzeigen auf der Symbolleiste Project Manager oder mit der Tastenkombination Strg + Alt + E anzeigen lassen.